Introduction to NumPy

As we discussed previously, the Python programming language provides a rich set of data structures such as the list, tuple, dictionary, and string, which can greatly simplify common programming tasks. Of these structures, all but the string are heterogeneous, which means they can hold data of different types. This flexibility comes at a cost, however, as it is more expensive in both computational time and storage to maintain an arbitrary collection of data than to hold a pre-defined set of data.

Optional: NumPy Implementation

(Advanced: Optional) For example, the Python list is implemented (in the Cython implementation) as a variable length array that contains pointers to the objects held in the array. While flexible, it takes time to create, resize, and iterate over, even if the data contained in the list is homogenous. Also, even though you can create multiple-dimensional lists, creating and working with them is neither simple or intuitive. Yet, many applications require multi-dimensional representation; for example, location on the surface of the Earth or pixel properties in an image.

Thus, these data structures clearly are not designed or optimized for data intensive computing. Scientific and engineering computing applications have a long history of using optimized data structures and libraries, including codes written in C, Fortran, or MatLab. These applications expect to have vector and matrix data structures and optimized algorithms that can leverage these structures seamlessly. Fortunately, since many data science applications, including statistical and machine learning, are built on this academic legacy, a community of open source developers have built the Numerical Python (NumPy) library, a fundamental numerical package to facilitate scientific computing in Python.

NumPy Array

NumPy is built around a new, n-dimensional array (ndarray) data structure that provides fast support for numerical computations. This data type for objects stored in the array can be specified at creation time, but the array is homogenous. This array can be used to represent a vector (one-dimensional set of numerical values) or matrix (multiple-dimensional set of vectors). Furthermore, NumPy provides additional benefits built on top of the array object, including masked arrays, universal functions, sampling from random distributions, and support for user-defined, arbitrary data-types that allow the array to become an efficient, multi-dimensional generic data container.

Is NumPy Worth Learning?

Despite the discussion in the previous section, you might be curious if the benefits of learning NumPy are worth the effort of learning to effectively use a new Python data structure, especially one that is not part of the standard Python distribution. In the end, you will have to make this decision, but there are several definite benefits to using NumPy:

  1. NumPy is much faster than using a list.
  2. NumPy is generally more intuitive than using a list.
  3. NumPy is used by many other libraries like SciPy, MatPlotLib, and Pandas.
  4. NumPy is part of the standard data science Python distribution.

NumPy is a very powerful library, with a rich and detailed user guide. Every time I look through the documentation, I learn new tricks. Furthermore, NumPy is the foundation upon which other popular Python modules, such as Pandas and Seaborn, are based. The time you spend learning to use this library properly will be amply rewarded. In the rest of this IPython notebook, we will introduce many of the basic NumPy features, but to fully master this library you will need to spend time reading the documentation and trying out the full capabilities of the library.

To demonstrate the first two points, consider the programming task of computing basic mathematical functions on a large number of data points. In the first code block, we first import both the math library and the numpy library. Second, we define two constants: size, which is the number of data points to process, and delta, which is a floating point offset we add to the array elements. You can change these two parameters to see how the performance of the different approaches varies. Finally, we create the list and the NumPy array that we will use in the next few codes blocks:

In [1]:
import math
import numpy as np

size = 100000
delta = 1.0E-2

aList = [(x + delta) for x in range(size)]
anArray = np.arange(size) + delta

print(aList[2:6])
print(anArray[2:6])

[2.01, 3.01, 4.01, 5.01]
[2.01 3.01 4.01 5.01]

At this point, we have created and populated both data structures, and you have seen that they are both indexed in the same manner, meaning it is probably easier to learn and use NumPy arrays than you might have thought. Next, we can apply several standard mathematical functions to our list, creating new lists in the process. To determine how long these operations take, we use the IPython %timeit magic function, which will, by default, run the code contained on the rest of the line multiple times and report the average best time.

In [2]:
%timeit [math.sin(x) for x in aList]
%timeit [math.cos(x) for x in aList]
%timeit [math.log(x) for x in aList]

12.1 ms ± 623 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
11.6 ms ± 394 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
13.2 ms ± 232 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

As you can see, to create these new list objects, we apply the mathematical function to every angle in the original list. These operations are fairly fast and all roughly constant in time, demonstrating the overall speed of list comprehensions in Python. Now we will try doing the same thing by using the NumPy library.

In [3]:
%timeit np.sin(anArray)
%timeit np.cos(anArray)
%timeit np.log10(anArray)

2.74 ms ± 66.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
2.71 ms ± 67 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
2.16 ms ± 110 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

First, the creation of each of these new arrays was much faster, nearly a factor of ten in each case! (Actual results will depend on the host computer and Python version.) Second, the operations themselves were arguably simpler both to write and to read, as the function is applied to the data structure itself and not each individual element. But perhaps we should compare the results to ensure they are the same.

In [4]:
l = [math.sin(x) for x in aList]
a = np.sin(anArray)

print("Python List: ", l[2:10:3])
print("NumPY array:", a[2:10:3])

print("Difference = ", a[5:7] - np.array(l[5:7]))
      
# Now create a NumPy array from a Python list
%timeit np.sin(aList)

Python List:  [0.905090563325201, -0.9560397542711181, 0.9878538030350801]
NumPY array: [ 0.90509056 -0.95603975  0.9878538 ]
Difference =  [0. 0.]
4.84 ms ± 72.9 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

As the previous code block demonstrates, the NumPy results agree with the standard Python results, although the NumPy results are more conveniently displayed. As a last test, we create a new NumPy array from the original Python list by applying the np.sin function, which, while not as fast as the pure NumPy version, is faster than the Python version and easier to read.

Now we will change gears and introduce the NumPy library.

Creating an Array

NumPy arrays, which are instances of the ndarray class, are statically-typed, homogenous data structures that can be created in a number of different ways. You can create an array from an existing Python list or tuple, or use one of the many built-in NumPy convenience methods:

  • empty: Creates a new array whose elements are uninitialized.
  • zeros: Creates a new array whose elements are initialized to zero.
  • ones: Creates a new array whose elements are initialized to one.
  • empty_like: Creates a new array whose size matches the input array and whose values are uninitialized.
  • zero_like: Creates a new array whose size matches the input array and whose values are initialized to zero.
  • ones_like: Creates a new array whose size matches the input array and whose values are initialized to unity.
In [5]:
# Make and print out simple NumPy arrays

print(np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]))

print("\n", np.empty(10))
print("\n", np.zeros(10))
print("\n", np.ones(10))
print("\n", np.ones_like(np.arange(10)))

[0 1 2 3 4 5 6 7 8 9]

 [0.0e+000 4.9e-324 9.9e-324 1.5e-323 2.0e-323 2.5e-323 3.0e-323 3.5e-323
 4.0e-323 4.4e-323]

 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]

 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

 [1 1 1 1 1 1 1 1 1 1]

We can also create NumPy arrays that have specific initialization patterns. For example, the arange(start, end, stride) method works like the normal Python range method, creating an array whose elements begin with the start parameter. Subsequent elements are incremented successively by the stride parameter, stopping when the end parameter would either be reached or surpassed. As was the case with the range method, the start and stride parameters are optional, defaulting to zero and one, respectively, and the end value is not included in the array.

In [6]:
# Demonstrate the np.arange method

print(np.arange(10))
print(np.arange(3, 10, 2))

[0 1 2 3 4 5 6 7 8 9]
[3 5 7 9]

NumPy also provides two convenience methods that take a similar form but assign values to the elements that are evenly spaced. The first method is the linspace(start, end, num) method, which creates num elements and assigns values that are linearly spaced between start and end.

The second method, logspace(start, end, num), creates num elements and assigns values that are logarithmically spaced between start and end. The num parameter is optional and defaults to fifty. Unlike the arange method, these two methods are inclusive, which means both the start and end parameters are included as elements in the new array. There is an optional parameter called base that you can use to specify the base of the logarithm used to create the intervals. By default, this value is 10, making the intervals log10 spaced.

In [7]:
# Demonstrate linear and logarthmic array creation.

print("Linear space bins [0, 10] = {}\n".format(np.linspace(0, 10, 4)))

print("Default linspace bins = {}\n".format(len(np.linspace(0,10))))


print("Log space bins [0, 1] = {}\n".format(np.logspace(0, 1, 4)))

print("Default linspace bins = {}\n".format(len(np.logspace(0,10))))

Linear space bins [0, 10] = [ 0.          3.33333333  6.66666667 10.        ]

Default linspace bins = 50

Log space bins [0, 1] = [ 1.          2.15443469  4.64158883 10.        ]

Default linspace bins = 50

Array Attributes

Each NumPy array has several attributes that describe the general features of the array. These attributes include the following:

  • ndim: Number of dimensions of the array (previous examples were all unity)
  • shape: The dimensions of the array, so a matrix with n rows and m columns has shape equal to (n, m)
  • size: The total number of elements in the array. For a matrix with n rows and m columns, the size is equal to the product of $n \times m$
  • dtype: The data type of each element in the array
  • itemsize: The size in bytes of each element in the array
  • data: The buffer that holds the array data

Array Data Types

NumPy arrays are statically-typed, thus their data type is specified when they are created. The default data type is float, but the type can be specified in several ways. First, if you use an existing list (as we did in the previous code block) or array to initialize the new array, the data type of the previous data structure will be used. If a heterogeneous Python list is used, the greatest data type will be used in order, guaranteeing that all values will be safely contained in the new array. If using a NumPy function to create the new array, the data type can be specified explicitly by using the dtype argument, which can either be one of the predefined built-in data types or a user defined custom data type.

The full list of built-in data types can be obtained from the np.sctypeDict.keys() method; but for brevity, we list some of the more commonly used built-in data types below, along with their maximum size in bits, which constrains the maximum allowed value that may be stored in the new array:

  • Integer: int8, int16, int32, and int64
  • Unsigned Integer: uint8, uint16, uint32, and uint64
  • Floating Point: float16, float32, float64, and float128

Other data types include complex numbers, byte arrays, character arrays, and date/time arrays.

To check the type of an array, you can simply access the array's dtype attribute. A ValueError exception will be thrown if you try to assign an incompatible value to an element in an array.

In [8]:
# Access our previously created array's data type 

a.dtype
Out[8]:
dtype('float64')

As previously declared, trying to assign the wrong data type to a NumPy array will throw a ValueException, as shown in the following figure (note: you can repeat this on your own in a new code cell).

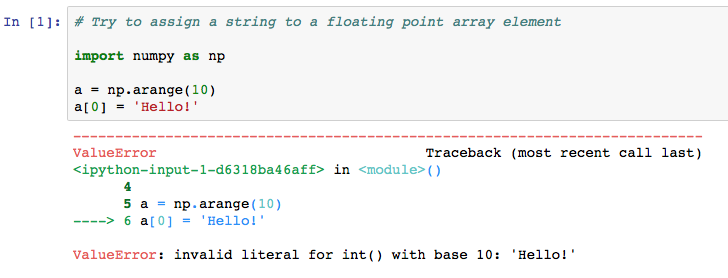
NumPy ValueException

Multidimensional Arrays

NumPy supports multidimensional arrays, although for simplicity we will rarely discuss anything other than two- or three-dimensional arrays. We will defer a discussion of working with multi-dimensional arrays by using NumPy to a subsequent lesson in this course.

Indexing Arrays

NumPy supports many different ways to access elements in an array. Elements can be indexed or sliced in the same way a Python list or tuple can be indexed or sliced, as demonstrated in the following code cell.

In [9]:
a = np.arange(9)
print("Original Array = ", a)

a[1] = 3
a[3:5] = 4
a[0:6:2] *= -1

print("\nNew Array = ", a)

Original Array =  [0 1 2 3 4 5 6 7 8]

New Array =  [ 0  3 -2  4 -4  5  6  7  8]

Special Indexing

NumPy also provides several other special indexing techniques. The first such technique is the use of an index array, where you use an array to specify the elements to be selected. The second technique is a Boolean mask array. In this case, the Boolean array is the same size as the primary NumPy array, and if the element in the mask array is True, the corresponding element in the primary array is selected, and vice-versa for a False mask array element. These two special indexing techniques are demonstrated in the following two code cells.

In [10]:
# Demonstration of an index array

a = np.arange(10)

print("\nStarting array:\n", a)
print("\nIndex Access: ", a[np.array([1, 3, 5, 7])])

Starting array:
 [0 1 2 3 4 5 6 7 8 9]

Index Access:  [1 3 5 7]
In [11]:
# Demonstrate Boolean mask access

# Simple case

a = np.arange(10)
print("Original Array:", a)

print("\nMask Array: ", a > 4)

# Now change the values by using the mask

a[a > 4] = -1.0
print("\nNew Array: ", a)

Original Array: [0 1 2 3 4 5 6 7 8 9]

Mask Array:  [False False False False False  True  True  True  True  True]

New Array:  [ 0  1  2  3  4 -1 -1 -1 -1 -1]

Random Data

NumPy has a rich support for random number generation, which can be used to create and populate an array of a given shape and size. NumPy provides support for sampling random values from over 30 different distributions including the binomial, normal, and poisson (we will discuss distribution functions in subsequent lessons). There are also special convenience functions to simplify the sampling of random data over the uniform or normal distributions. These techniques are demonstrated in the following code cell.

In [12]:
# Create arrays of random data from different distributions

print("Uniform sampling, integers [0, 1): {}".format(np.random.randint(0, 10, 5)))
print("Uniform sampling [0, 1): {}".format(np.random.rand(5)))
print("Normal sampling (0, 1) : {0}".format(np.random.randn(5)))

Uniform sampling, integers [0, 1): [7 9 7 1 4]
Uniform sampling [0, 1): [0.03940366 0.17357534 0.82906679 0.89069131 0.57856134]
Normal sampling (0, 1) : [ 1.18137452  1.00074096  1.90949477 -1.45488541  2.2543386 ]

Basic Operations

NumPy arrays naturally support basic mathematical operations, including addition, subtraction, multiplication, division, integer division, and remainder, allowing you to easily combine a scalar (a single number) with a vector (a one-dimensional array), or a matrix (a multi-dimensional array). In the next code block, we first create a one-dimensional array, and subsequently operate on this array to demonstrate how to combine a scalar with a vector.

In [13]:
# Create and use a vector
a = np.arange(10)

print(a)
print("\n", (2.0 * a + 1)/3)
print("\n", a%2)
print("\n", a//2)

[0 1 2 3 4 5 6 7 8 9]

 [0.33333333 1.         1.66666667 2.33333333 3.         3.66666667
 4.33333333 5.         5.66666667 6.33333333]

 [0 1 0 1 0 1 0 1 0 1]

 [0 0 1 1 2 2 3 3 4 4]

Student Exercise

In the empty Code cell below, first create a one-dimensional NumPy array by using the arange function of the integers zero to ten, inclusive. Next, perform the following basic math operations on this new array and display only the final result. First, add two to every element. Second, multiply the result by five. Finally, subtract seven. Next, create a second array of eleven, randomly selected integers between zero and ten, and multiply this new array by the original array, displaying the result.

In [ ]:

Summary Functions

NumPy provides convenience functions that can quickly summarize the values of an array, which can be very useful for specific data processing tasks (note that we will cover descriptive statistics in a subsequent lesson). These functions include basic statistical measures (mean, median, var, std, min, and max), the total sum or product of all elements in the array (sum, prod), as well as running sums or products for all elements in the array (cumsum, cumprod). The last two functions actually produce arrays that are of the same size as the input array, where each element is replaced by the respective running sum/product up to and including the current element. Another function, trace, calculates the trace of an array, which simply sums up the diagonal elements in the multi-dimensional array.

In [14]:
# Demonstrate data processing convenience functions

# Make an array = [1, 2, 3, 4, 5]
a = np.arange(1, 6)

print("Mean value = {}".format(np.mean(a)))
print("Median value = {}".format(np.median(a)))
print("Variance = {}".format(np.var(a)))
print("Std. Deviation = {}\n".format(np.std(a)))

print("Minimum value = {}".format(np.min(a)))
print("Maximum value = {}\n".format(np.max(a)))

print("Sum of all values = {}".format(np.sum(a)))
print("Running cumulative sum of all values = {}\n".format(np.cumsum(a)))

print("Product of all values = {}".format(np.prod(a)))
print("Running product of all values = {}\n".format(np.cumprod(a)))

Mean value = 3.0
Median value = 3.0
Variance = 2.0
Std. Deviation = 1.4142135623730951

Minimum value = 1
Maximum value = 5

Sum of all values = 15
Running cumulative sum of all values = [ 1  3  6 10 15]

Product of all values = 120
Running product of all values = [  1   2   6  24 120]

Universal Functions

NumPy also includes methods that are universal functions or ufuncs that are vectorized and thus operate on each element in the array, without the need for a loop. You have already seen examples of some of these functions at the start of this IPython Notebook when we compared the speed and simplicity of NumPy versus normal Python for numerical operations. These functions almost all include an optional out parameter that allows a pre-defined NumPy array to be used to hold the results of the calculation, which can often speed-up the processing by eliminating the need for the creation and destruction of temporary arrays. These functions will all still return the final array, even if the out parameter is used.

NumPy includes over sixty ufuncs that come in several different categories:

  • Math operations, which can be called explicitly or simply implicitly when the standard math operators are used on NumPy arrays. Example functions in this category include add, divide, power, sqrt, log, and exp.
  • Trigonometric functions, which assume angles measured in radians. Example functions include the sin, cos, arctan, sinh, and deg2rad functions.
  • Bit-twiddling functions, which manipulate integer arrays as if they are bit patterns. Example functions include the bitwise_and, bitwise_or, invert, and right_shift.
  • Comparison functions, which can be called explicitly or implicitly when using standard comparison operators that compare two arrays, element-by-element, returning a new array of the same dimension. Example functions include greater, equal, logical_and, and maximum.
  • Floating functions, which compute floating point tests or operations, element-by-element. Example functions include isreal, isnan, signbit, and fmod.

Look at the official NumPy ufunc reference guide for more information on any of these functions, for example, the isnan function, since the user guide has a full breakdown of each function and sample code demonstrating how to use the function.

In the following code blocks, we demonstrate several of these ufuncs.

In [15]:
b = np.arange(1, 10)

print('original array:\n', b)

c = np.sin(b)

print('\nnp.sin : \n', c)

print('\nnp.log and np.abs : \n', np.log10(np.abs(c)))

print('\nnp.mod : \n', np.mod(b, 2))

print('\nnp.logical_and : \n', np.logical_and(np.mod(b, 2), True))

original array:
 [1 2 3 4 5 6 7 8 9]

np.sin : 
 [ 0.84147098  0.90929743  0.14112001 -0.7568025  -0.95892427 -0.2794155
  0.6569866   0.98935825  0.41211849]

np.log and np.abs : 
 [-0.07496085 -0.04129404 -0.85041141 -0.12101744 -0.01821569 -0.55374951
 -0.18244349 -0.00464642 -0.38497791]

np.mod : 
 [1 0 1 0 1 0 1 0 1]

np.logical_and : 
 [ True False  True False  True False  True False  True]
In [16]:
# Demonstrate Boolean tests with operators

d = np.arange(9)

print("Greater Than or Equal Test: \n", d >= 5)

# Now combine to form Boolean Matrix

np.logical_and(d > 3, d % 2)

Greater Than or Equal Test: 
 [False False False False False  True  True  True  True]
Out[16]:
array([False, False, False, False, False,  True, False,  True, False])

Masked Arrays

NumPy provides support for masked arrays, where certain elements can be masked based on some criterion and ignored during subsequent calculations (i.e., these elements are masked). Masked arrays are in the numpy.ma package, and simply require a masked array to be created from a given array and a condition that indicates which elements should be masked. This new masked array can be used as a normal NumPy array, except the masked elements are ignored. NumPy provides operations for masked arrays, allowing them to be used in a similar manner as normal NumPy arrays.

You can also impute missing (or bad) values by using a masked array, and replacing masked elements with a different value, such as the mean value. Masked arrays can also be used to mask out bad values in a calculation such as divide-by-zero or logarithm of zero, and a masked array will ignore error conditions during standard operations, making them very useful since they operate in a graceful manner.

In [17]:
# Create and demonstrate a masked array

import numpy.ma as ma

x = [0.,1.,-9999.,3.,4.]
print("Original array = :", x)


mx = ma.masked_values (x, -9999.)
print("\nMasked array = :", mx)


print("\nMean value of masked elements:", mx.mean())
print("\nOperate on unmasked elements: ", mx - mx.mean())
print("\n Impute missing values (using mean): ", mx.filled(mx.mean())) # Imputation

Original array = : [0.0, 1.0, -9999.0, 3.0, 4.0]

Masked array = : [0.0 1.0 -- 3.0 4.0]

Mean value of masked elements: 2.0

Operate on unmasked elements:  [-2.0 -1.0 -- 1.0 2.0]

 Impute missing values (using mean):  [0. 1. 2. 3. 4.]
In [18]:
# Create two arrays with masks
x = ma.array([1., -1., 3., 4., 5., 6.], mask=[0,0,0,0,1,0])
y = ma.array([1., 2., 0., 4., 5., 6.], mask=[0,0,0,0,0,1])

# Now take square root, ignores div by zero and masked elements.
print(np.sqrt(x/y))

[1.0 -- -- 1.0 -- --]

/opt/conda/envs/py36/lib/python3.6/site-packages/ipykernel_launcher.py:6: RuntimeWarning: invalid value encountered in sqrt
In [19]:
# Now try some random data

d = np.random.rand(1000)

# Now mask for values within some specified range (0.1 to 0.9)
print("Masked array mean value: ", ma.masked_outside(d, 0.1, 0.9).mean())

Masked array mean value:  0.5064199853933288

NumPy File Input/Output

NumPy has support for reading or writing data to files. Of these methods, two of the most useful are the loadtxt method and the genfromext method, each of which allow you to easily read data from a text file into a NumPy array. The primary difference is that the genfromtxt method can handle missing data, while the loadtxt cannot. Both methods allow you to specify the column delimiter, easily skip header or footer rows, specify which columns should be extracted for each row, and allow you to unpack the row so that each column goes into a separate array.

For example, the following code snippet demonstrates how to use the loadtxt method to pull out the second and fourth columns from the fin file handle, where the file is assumed to be in CSV format. The data is persisted into the a and b NumPy arrays.

a, b = np.loadtxt(fin, delimeter = ',', usecols=(1, 3), unpack=True)

We demonstrate the genfromtxt method in the following code block, where we first create the test data file before reading that data back into a NumPy array.

In [20]:
# First write data to a file using Unix commands. 
info = "1, 2, 3, 4, 5 \n 6, 7, 8, 9, 10"
with open("test.csv", 'w') as fout:
    print(info, file=fout)

# Now we can read it back into a NumPy array.
d = np.genfromtxt("test.csv", delimiter=",")

print("New Array = \n", d)

New Array = 
 [[ 1.  2.  3.  4.  5.]
 [ 6.  7.  8.  9. 10.]]

In addition to the normal Python help function, NumPy provides a special lookup function that will search the NumPy library for classes, types, or methods that match the search string passed to the function. This can be useful for finding specific information given a general concept, or to learn more about related topics by performing a search. For example, the following function call would display all relevant NumPy information for 'masked array'.

np.lookfor('masked array')

Student Exercise

In the empty Code cell below, first create a one-dimensional NumPy array of the even integers from 20 to 42, inclusive. Next, apply a ufunc to compute the fourth power of each element in this array. Divide each element in this array by 11, and print out the resulting elements, one element per line.

In [ ]:

Ancillary Information

The following links are to additional documentation that you might find helpful in learning this material. Reading these web-accessible documents is completely optional.

  1. NumPy tutorial
  2. NumPy cheatsheet
  3. NumPy lecture notes
  4. NumPy notebook demo
  5. The NumPy chapter from the book Python Data Science Handbook by Jake VanderPlas

© 2017: Robert J. Brunner at the University of Illinois.

This notebook is released under the Creative Commons license CC BY-NC-SA 4.0. Any reproduction, adaptation, distribution, dissemination or making available of this notebook for commercial use is not allowed unless authorized in writing by the copyright holder.