Introduction to Descriptive Statistics¶
One of the most basic tasks in data analytics, particularly for large data sets, is describing a data set by a small number of statistical quantities. For example, we may wish to know the average income in a geographic region, or the general spread about this average income. In this notebook, we introduce statistical quantities that can be used to describe a (one-dimensional) data set and to enable comparisons between data sets. Fundamentally, this task includes computing
- a measure of location of centrality,
- a measure of variability or spread,
- measures of the distribution, and
- measures of the distribution shape.
In addition, we also will look at measuring these quantities when the data have been measured with different precision (or have different errors) before finally concluding with a discussion on populations and samples.
First, however, we include our standard imports and provide a brief exploration of a demo dataset before generating a NumPy array for our total_bill column to simplify computing descriptive statistics.
# Standard imports
import numpy as np
import scipy as sp
import pandas as pd
import seaborn as sns
pd.options.display.max_rows = 10
# Load the Tips Data
tips = sns.load_dataset("tips")
# Display first few rows
tips.head(5)
# Convert the total_bill column to a NumPy array
data = tips.total_bill.values
data[10:20]
Measures of Location (Centrality)¶
Mean¶
Given a data set, for example, the total_bill column in the tips data set, the first step is often to compute a typical value, in this case the typical bill. The standard approach to this task is to compute the average or (arithmetic) mean ($\mu$ or $\overline{x}$):
Computing this in Python is generally quite simple, and most data structures (including both Pandas and NumPy) include helper functions for comptuing this and other descriptive statistics. For example, we can compute the mean value for the total_bill column in the tips data:
tips[['total_bill']].mean()
In subsequent lessons, we will explore theoretical distributions, such as the Normal or Gaussian distribution, for which the arithmetic mean plays an important role. As a descriptive statistic, however, other means can also be computed, including the geometric and harmonic means:
- Geometric mean: The n-th root of a set of values
- Harmonic mean: The mean of ratio quantities
More generally, we can use the NumPy module (on the data array) to compute the arithmetic mean and other descriptive statistics, as demonstrated in the following code cell.
# We compute three different mean quantities
print('Mean Value = {:6.4f}'.format(np.mean(data)))
print('Geometric Mean Value = {:6.4f}'.format(sp.stats.gmean(data)))
print('Harmonic Mean Value = {:6.4f}'.format(sp.stats.hmean(data)))
The mean (or average) is a commonly used descriptive statistic. However, some data are distributed in ways that make the mean a poor measure for the typical value. For example, if data are bi-modal (with lots of low values and lots of high values) the mean will typically lie between these two clumps of data. Likewise, this can occur if a data set has a number of outliers at one end of a range (such as sales contracts that are much higher than the rest of the sales contracts in a list). In this case, other measures can provide more robust estimates. Some of the more common such measures include the median, the mode, and trimmed mean.
Median¶
The median is conceptually an easy measure of centrality; half the data lie above and below the median. Thus, to compute the median you first sort the data and select the middle element. While conceptually simple, in practice computing the median is complicated by several issues:
- We need to sort the data, which is challenging for big data (and also implies the data can be sorted).
- For a data set with an even number of values there is no middle value.
In the last case, for example, given the list of points [0, 1, 2, 3, 4, 5], we can use three different techniques to compute a median:
a. average the two middle values (median=2.5),
b. take the lower of the two middle values (median=2), or
c. take the higher of the two middle values (median=3).
Often, a Python module by default employs the first technique (average the two middle values), although, as demonstrated below, exceptions to this do occur, such as in the built-in Python statistics module, which can return any of these three values.
Mode¶
The mode is simply the most common value in a data set. Often, a mode makes the most sense when the data have been binned, in which case the data have been aggregated and it becomes simple to find the bin with the most values (we will see this in a later lesson on distributions). A mode can also make sense when data are categorical, or explicitly limited to a discrete set of values. When calculating the mode (or modal value), we also have the number of times this value occurred, as demonstrated below.
Trimmed Mean¶
One simple technique to compute a more robust, average value is to trim outlier points before calculating the mean value, producing a trimmed mean. The trimming process generally eliminates either a set number of points from the calculation, or any values that are more extreme than a certain range (such as three standard deviations from the untrimmed mean). In NumPy, the latter approach is used, and a lower and upper limit can be applied to eliminate values outside this range from being used in the computation of the trimmed mean.
print('Median Value = {:6.4f}'.format(np.median(data)))
mode = sp.stats.mode(data)
print('Modal Value = {0:6.4f}, occured {1} times.'.format(mode[0][0], mode[1][0]))
low = 12.5
up = 27.5
tm = sp.stats.tmean(data, (low, up))
print('Trimmed Mean = {0:6.4f} with bounds = {1:4.2f} : {2:4.2f}'.format(tm, low, up))
If our data is stored in a traditional Python data structure, such as a list, we can use the built-in statistics module to compute these quantities (as well as the lower and upper median), as demonstrated below. This includes an explicit demonstration of calculating the mode for a categorical data type.
# Use the built-in statistics module for a list
import statistics as st
#convert NumPy array to a list
data_list = list(data)
# Compute and display basic statistics
print('Mean Value = {:6.4f}'.format(st.mean(data_list)))
print('Median Value = {:6.4f}'.format(st.median(data_list)))
print('Mode Value = {:6.4f}'.format(st.mode(data_list)))
# Categorical data example
color_data = ['red', 'blue', 'blue', 'brown', 'brown', 'brown']
print('Modal color = {}'.format(st.mode(color_data)))
# High and low Median example
print('Median (low) Value = {:6.4f}'.format(st.median_low(data_list)))
print('Median Value = {:6.4f}'.format(st.median(data_list)))
print('Median (high) Value = {:6.4f}'.format(st.median_high(data_list)))
Student Exercise
In the empty Code cell below, write and execute code to compute the mean and median for the total_bill column, separately for those rows corresponding to lunch and dinner. What do these values suggest about the typical lunch or dinner party?
Measures of Variability (Dispersion)¶
Once we have a measure for the central location of a data set, the next step is to quantify the spread or dispersion of the data around this location. Inherent in this process is the computation of a distance between the data and the central location. Variations in the distance measurement can lead to differences in variability measures, which include the following dispersion measurements:
- Range
- Mean deviation
- Mean absolute deviation
- Variance
- Standard deviation
Range¶
Of these, the simplest is a range measurement, which is simply the difference between two characteristic values. Often these are the minimum and maximum values in a data set. While simple, this provides little insight into the true spread or dispersion of the data, in particular, about the centrality measure (since the mean might lie anywhere between the maximum and minimum values).
Mean Deviation¶
Each of the remaining four dispersion measurements are made with respect to a location measure, which is typically the mean value. Thus, the mean deviation is typically measured with respect to the mean value, as shown by the following formula:
\begin{equation} \textrm{Mean Deviation} = \frac{\sum_{i=1}^N (x_i - \overline{x})}{N} \end{equation}While simple, one sums up the deviations from the mean value and divides by the number of points, this measure cancels out high and low measurements, producing a small value measure (which can be zero) for the spread of the data around the mean value. This problem can be overcome by using two different techniques: summing absolute deviations or summing the square of the deviations, which leads to the last three measures.
Mean Absolute Deviation¶
First, if we sum up the absolute deviations, we generate a sum of intrinsically positive values. This mean absolute deviation is also known as an $l1-$norm, or Manhattan norm. This norm finds uses in a number of situations, including in machine learning. The formula for the mean absolute deviation is simple:
\begin{equation} \textrm{Mean Absolute Deviation} = \frac{\sum_{i=1}^N |x_i - \overline{x}|}{N} \end{equation}Variance¶
Second, if we sum up the square of the deviations from the mean, we also end up with a sum of intrinsically positive numbers, which is known as the $l2-$norm, or the Euclidean norm. This norm should be familiar, as it is used in the Pythagorean formula, and it is also used in machine learning.
The formula for the mean absolute deviation is simple:
\begin{equation} \textrm{Variance} = \frac{\sum_{i=1}^N (x_i - \overline{x})^2}{N} \end{equation}Standard Deviation¶
One concern with the variance, however, is that the units of variance are the square of the original units (for example, length versus length * length). To enable the measure of the variability around the mean to be compared to the mean, we generally will use the standard deviation, which is simply the square root of the variance:
\begin{equation} \textrm{Standard Deviation} = \sigma = \sqrt{\left(\frac{\sum_{i=1}^N (x_i - \overline{x})^2}{N}\right)} \end{equation}Coefficient of Variation¶
The value of a dispersion measure can be confusing. On its own, a large or small dispersion is less informative than a dispersion measure combined with a location measure. For example, a dispersion measure of 10 means something different if the mean is 1 versus 100. As a result, the coefficient of variation is sometimes used to encode the relative size of a dispersion to the mean:
\begin{equation} \textrm{Coefficient of Variation} = \frac{\textrm{Standard deviation}}{\textrm{Mean value}} = \frac{\sigma}{\mu} \end{equation}In the following code cells, we compute these quantities by using built-in functions from the NumPy module, our own computations for the mean deviation and mean absolute deviation, and demonstrate how to compute the variance and standard deviation by using the built-in statistics module on data stored in a list.
# Compute Range quantities
print('Maximum = {:6.4f}'.format(np.max(data)))
print('Minimum = {:6.4f}'.format(np.min(data)))
print('Range = {:6.4f}'.format(np.max(data) - np.min(data)))
print('Peak To Peak (PTP) Range = {:6.4f}\n'.format(np.ptp(data)))
# Compute deviations
tmp = data - np.mean(data)
n = data.shape[0]
print('Mean Deviation from Mean = {:6.4f}'.format(np.sum(tmp/n)))
print('Mean Absolute Deviation from Mean = {:6.4f}\n'.format(np.sum(np.absolute(tmp))/n))
# Use standard functions for variance
print('Variance = {:6.4f}'.format(np.var(data)))
print('Standard Deviation = {:6.4f}\n'.format(np.std(data)))
# Coefficient of Variation
print('Coefficient of Variation = {:6.4f}'.format(np.std(data)/np.mean(data)))
# Use Python's built-in statistics module
# Works with list data
print('Variance = {:6.4f}'.format(st.variance(data_list)))
print('Standard Deviation = {:6.4f}'.format(st.stdev(data_list)))
Student Exercise
In the empty Code cell below, write and execute code to compute the mean absolute deviation and standard deviation for the total_bill column, separately for those rows corresponding to lunch and dinner. What do these values suggest about the typical lunch or dinner party? Also, compare the coefficient of variation for the same data. Do these values also make sense?
Measures of Distribution¶
While useful, measures of location and dispersion are only two numbers. Thus, other techniques exist for analytically quantifying a distribution of data. Fundamentally, these techniques all rely on sorting the data and finding the value below which a certain percentage of data lie. In this manner, one percentile would correspond to one percent of the data, while the median would correspond to fifty percent of the data. Formally, the following pre-defined measures are commonly used:
- Percentiles: Divides the data into one percent chunks, the value indicates which percentile is of interest
- Deciles: Divides the data into ten chunks, each containing 10% of the data
- Quantiles: Divides the data into five chunks, each containing 20% of the data
- Quartiles: Divides the data into four chunks, each containing 25% of the data
With NumPy we just use percentile function for all of these and specify the appropriate value for the percentile. Thus for the second decile, we specify np.percentile(data, 20). The following code cell demonstrates some of the more common values.
# Demonstrate percentile with the Median
print('Median (via percentile) = {:6.4f}'.format(np.percentile(data, 50)))
# Compute quartiles
print('First Quartile = {:6.4f}'.format(np.percentile(data, 25)))
print('Second Quartile = {:6.4f}'.format(np.percentile(data, 50)))
print('Third Quartile = {:6.4f}'.format(np.percentile(data, 75)))
print('Fourth Quartile = {:6.4f}'.format(np.percentile(data, 100)))
# Interquartile range is sometimes used as a dispersion measure
print('Quartile Range = {:6.4f}'.format(np.percentile(data, 75) - np.percentile(data, 25)))
# Compute quantiles
print('First Quantile = {:6.4f}'.format(np.percentile(data, 20)))
print('Second Quantile = {:6.4f}'.format(np.percentile(data, 40)))
print('Third Quantile = {:6.4f}'.format(np.percentile(data, 60)))
print('Fourth Quantile = {:6.4f}'.format(np.percentile(data, 80)))
Student Exercise
In the empty Code cell below, write and execute code to compute the interquartile range for the total_bill column, separately for those rows corresponding to lunch and dinner. What do these values suggest about the typical lunch or dinner party? Also, compute all quantiles for these same data, and compare the spread of the data in both data sets.
Weighted Statistics¶
Often the data we analyze should be treated differently. For example, if the data have associated errors, some data will have smaller errors and thus be more precise measurements. Likewise, in some situations, we will have more data of one class (such as lunch receipts) when compared to other classes (like dinner receipts). As a result, we will want to weight the data appropriately to handle the additional information or to emphasize special cases of the analysis.
In these cases, given a set of data ($x_i$) with associated weights ($w_i$), we can compute weighted measures for the mean ($\mu_w$) and standard deviation ($\sigma_w$). In both cases, we simply weight the values appropriately and correct our normalization for the weights.
\begin{equation} \mu_w = \frac{\sum_{i=1}^N w_i x_i}{\sum_{i=1}^N w_i} \end{equation}\begin{equation} \sigma_w = \sqrt{\frac{\sum_{i=1}^N w_i (x_i - \mu_w)^2}{\sum_{i=1}^N w_i}} \end{equation}These calculations are demonstrated in Python in the following code cell, where we generate random weights. The NumPy module does provide a function to compute a weighted mean (average) but does not yet include a function for computing the weighted standard deviation; thus, we compute this quantity according to the previous formula and display the unweighted and weighted versions of these quantities.
import math
# generate random weights
w = np.random.uniform(size=data.shape)
# Compute weighted mean
wm = np.average(data, weights=w)
# Compute weighted standard deviation
wstd = math.sqrt(np.average((data - wm)**2, weights = w))
# Compute and display normal & weighted statistics
print('Mean = {:6.4f}'.format(np.sum(np.mean(data))))
print('Weighted Mean = {:6.4f}\n'.format(wm))
print('Standard Deviation = {:6.4f}'.format(np.std(data)))
print('Weighted Standard Deviation = {:6.4f}\n'.format(wstd))
Measures of Shape¶
In contrast to measures of the distribution, such as the percentile or quantile, there are several other pre-defined quantities that provide insight into the shape of a data set, especially in relation to the mean and standard deviation. The two most prominent such measures are the skewness and the kurtosis. The skewness measures the lack of symmetry with respect to the mean value. Values near zero indicate symmetric distributions, while larger values indicate increasing asymmetry. Kurtosis, on the other hand, measures the spread (or how wide the tails are) of a distribution relative to the Normal distribution. Small values of Kurtosis indicate data that are highly concentrated around the mean value, while large values of the kurtosis indicate data that are considerably more different than the mean value.
These quantities can easily be calculated in Python by using the appropriate functions from the Scipy module, as shown in the following code blocks.
skew = sp.stats.skew(data)
print('Skewness = {0:6.4f}'.format(skew))
kurt = sp.stats.kurtosis(data)
print('Kurtosis = {0:6.4f}'.format(kurt))
Population or Sample¶
To this point, we have focused on describing a data set as if it stood alone. For example, you might have access to the full financial statements of a company or information about every transaction that took place in a given market. In some cases, however, you may only have a subset of this full information. This may arise when the original data is very large and you simply want to explore a subset of the full data, or perhaps you were simply given a subset in order to ascertain any issues of problems.
Formally, this division can be described as being given either the full population or simply a sample. Traditional statistics, being developed many years ago when data sets were small and all calculations were done with pencil and paper, focused on using samples to make predictions (or estimates) of the full population. In practice, this introduces several new terms and small changes in calculating descriptive statistics. First, the originating data set is often called the parent population. Second, the process of selecting data from the parent population is known as sampling. This relationship is encoded in the following figure:
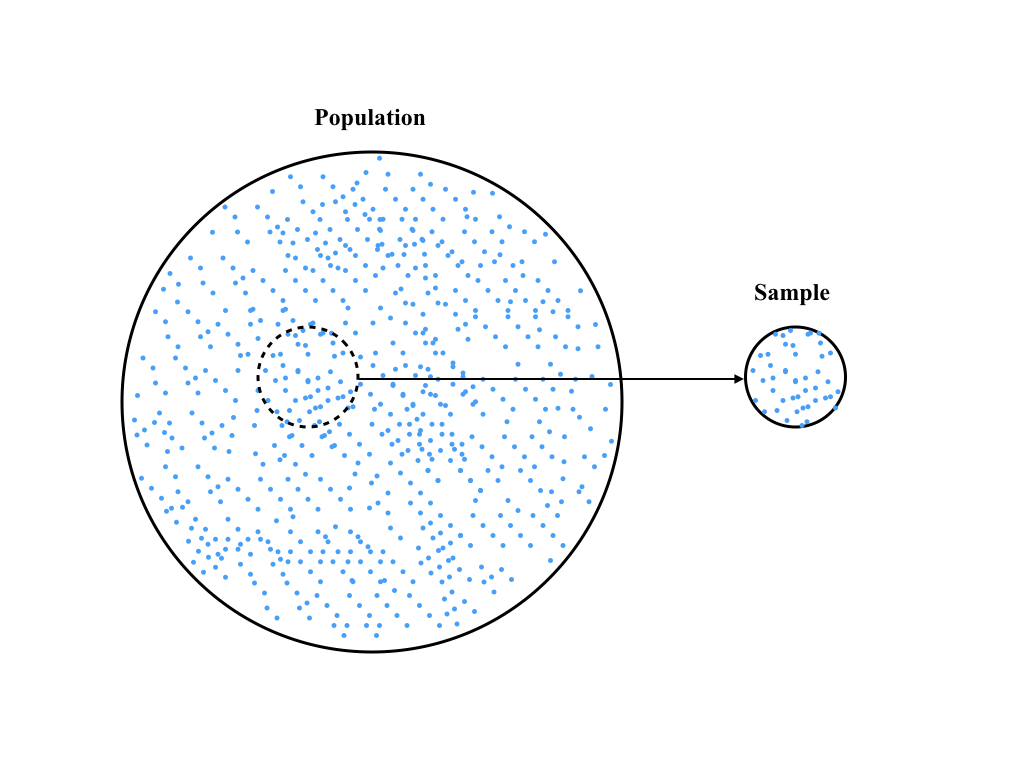
When using a sample to describe the parent population, we must account for the fact that we are using limited information to describe something (potentially) much larger. Thus, when we use a sample to estimate the mean value of the parent population, we have reduced the information content of our sample. This means that when we use this estimated mean value to compute the estimated standard deviation, we actually compute a less precise estimate. This is formalized by a concept known as degree of freedom, which is given by the number of data points in the sample, N, which is equal to the length of the data set in Python.
Thus, we can estimate the mean (or average) value of a parent population by computing the mean value of the sample ($\overline{x}$):
\begin{equation} \overline{x} = \frac{\sum_{i = 1}^N x_i}{N} \end{equation}Since we have now used the sample to estimate one descriptive statistic, the arithmetic mean of the parent population, we have reduced the degree of freedom in computing the variance or standard deviation of the parent population from the sample. Thus, we must divide the standard deviation estimate by $ N - 1 $, not $N$, as shown below:
\begin{equation} \textrm{var} = \frac{\sum_{i = 1}^N (x_i - \overline{x})^2}{N - 1} \end{equation}We often use the sample standard deviation ($s$), since this has the same units as the mean value, which is the square root of the variance:
\begin{equation} \textrm{s} = \sqrt{\frac{\sum_{i = 1}^N (x_i - \overline{x})^2}{N - 1}} \end{equation}To calculate this by using Python, we can simply pass in delta degrees of freedom parameter to the numpy.std method:
np.std(data, ddof=1)
Another statistic that is often of interest is the precision with which we can measure the mean value. Intuitively, as the number of points in our sample increases, the precision should increase (and the standard deviation decrease). This is formulated by the sample standard error, or SE, which measures the standard error in quantifying a statistic. Thus, if we want to know the precision in our measurement of the mean, we can compute the sample standard error of the mean. Formally, this value is computed by dividing the sample standard deviation by the square root of the number of data points in the sample:
\begin{equation} \textrm{SE} = \frac{s}{\sqrt{N}} \end{equation}Note that for large data sets, the difference in dividing by $N$ or $N - 1$ is minimal and we thus can often ignore the difference in practice.
# Compare population and sample standard deviations
print('Standard Deviation = {:6.4f}'.format(np.std(data)))
print('Sample Standard Deviation = {:6.4f}'.format(np.std(data, ddof=1)))
Ancillary Information¶
The following links are to additional documentation that you might find helpful in learning this material. Reading these web-accessible documents is completely optional.
- NumPy statistics documentation
- The Python Statistics module
- Blog article by Randal Olsen on statistical analysis with Pandas
- The exploratory data analysis chapter from the book Think Stats 2e by Allen Downey
© 2017: Robert J. Brunner at the University of Illinois.
This notebook is released under the Creative Commons license CC BY-NC-SA 4.0. Any reproduction, adaptation, distribution, dissemination or making available of this notebook for commercial use is not allowed unless authorized in writing by the copyright holder.